Allmogen och matematiska konstanter
I en diskussion i swnet.diverse fick jag orsak att (ur minnet) återge vad den kände brittiske filosofen, vetenskapsmannen, parlamentsledamoten, kroppsbyggaren, gentlemannen och godsägaren Icabod Thielly (1788-1863) skrev om matematiska konstanter, i sitt standardverk En skrift om tingens ordning.
Nedan följer de i sammanhanget relevanta avsnitten ur denna skrift, vilken jag sedan dess återigen -- och med stort intresse! -- studerat.
Följer kapitel 8 och 9 ur Icabod Thiellys En skrift om tingens ordning, del II:
| Perfekt låda c = 1 |
Lårk c =  /2 |
Perfekt burk c = 2 |
Buda c = e |
Perfekt låda c =  |
 a = b = 1 |
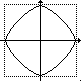 a = b = 1 |
 a = b = 1 |
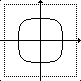 a = b = 0.6 |
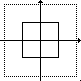 a = b = 0.5 |
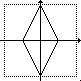 a = 0.5; b = 1 |
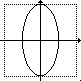 a = 0.5; b = 1 |
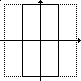 a = 0.5; b = 1 |
| Kärlet vi ämnar klassificera projiceras uppifrån, å ett cartesiskt koordinatsystem, så att den projicerade ytans tyngdpunkt hamnar i det cartesiska koordinatsystemets origo. Därefter minimeras, i minsta-kvadrat-bemärkelse, skillnaden mellan å ena sidan den projicerade ytans rand, och å andra sidan den speciella kurva som kan beskrivas av ekvationen | ||||||
| ||||||
Ifrågavarande minimering går till på så vis, att såväl kärlets rand som ekvationen
ovan först skrives på s.k. polär form, r = r( )
| ||||||
|
rkärl = f( - 0)
ra,b,c = g(a,b,c, )
| ||||||
| Därefter minimeras integralen | ||||||
| ||||||
|
med avseende på de fyra parametrarna a, b, c och 0.
|
| Nu studeras noga det vid minimeringen erhållna värdet för parametern c. (De övriga är ej lika väsentliga.) Det gäller att om | ||
| c < /2 eller e < c | är kärlet en låda! | |
| /2 < c < e | är kärlet en burk! | |
| I vissa speciella sällskap och sammanhang är en mera noggrann kategorisering givetvis nödvändig: | ||
| c < 1 | exflatulerad låda | |
| c = 1 | perfekt låda | |
| 1 < c < /2 | inflatulerad låda | |
| c = /2 | lårk | |
| /2 < c < 2 | exflatulerad burk | |
| c = 2 | perfekt burk | |
| 2 < c < e | exflatulerad burk | |
| c = e | buda | |
| e < c < | inflatulerad låda | |
| c = | perfekt låda | |
| Lårken och budan utgör två olika gränstillstånd mellan den exflatulerade burken och den inflatulerade lådan. |
Den metod, som diskuterades i kapitel åtta, för att fastställa huruvida
ett kärl är en burk eller en låda, används i praktiken givetvis i första hand
just för att klassificera olika kärl: En husmor, en köksa eller en husa som är
osäker huruvida ett visst kärl skall ställas bland burkarna eller bland lådorna, kan, medelst
den i kapitel åtta beskrivna metoden, enkelt klassificera sitt kärl, och
därefter ställa det på rätt plats, utan någon egentlig risk för felaktigheter.
 Figur: Allmoge
Ovan beskrivna förfarande förekommer dock närmast uteslutande i våra städer.
För vår allmoge och våra odalmän, å andra sidan, har metoden andra användnings- och
tillämpningsområden. Ty sällan eller aldrig har ju vår allmoge omedelbar tillgång
till vare sig matematiska tabeller eller
andra skrifter där
Om odalmannen avsåg att beräkna värdet av |
Artiklar av Samuel Sirén:
|
Däremot: Närhelst en odalman är tvungen att skaffa sig
kunskap om värdet av